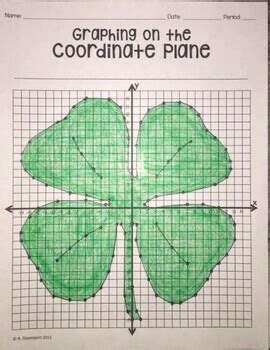
Have you ever looked at a blank sheet of graph paper and felt a mix of apprehension and excitement? Perhaps you're a parent trying to make math fun for your child, a teacher searching for that perfect St. Patrick's Day activity, or even a curious learner eager to explore the artistic side of mathematics. Whatever your journey, you’ve landed in the right place. Trust me, I’ve been there – staring at a jumble of numbers, wondering how they could possibly form something as beautiful as a shamrock. I remember one particularly frustrating evening trying to help my nephew with a graphing assignment, only to realize we were both making the same fundamental mistake with negative coordinates! If only I’d had a resource like this then, it would have saved us hours of head-scratching and turned a daunting task into a delightful discovery.
This isn't just an article; it's your comprehensive companion to mastering the coordinate plane shamrock graph printable. We’re going to demystify coordinate geometry, transform abstract numbers into vibrant visual art, and provide you with a treasure trove of ready-to-use printables and creative ideas. Whether you're a complete beginner taking your first steps into the world of x and y axes, or a seasoned educator looking for advanced strategies to engage your students, this guide is packed with actionable insights, personal experiences, and expert tips. Get ready to turn math into an adventure, one plotted point at a time!
---
Table of Contents

- [The Magic of the Coordinate Plane: A Beginner's Journey](#the-magic-of-the-coordinate-plane-a-beginners-journey)
- [Shamrock Graphing: From Concept to Clover](#shamrock-graphing-from-concept-to-clover)
- [Unlocking the Power of Printable Shamrock Graphs](#unlocking-the-power-of-printable-shamrock-graphs)
- [Creative Classroom & Home Activities with Shamrock Graphs](#creative-classroom-home-activities-with-shamrock-graphs)
- [Beyond the Basic Shamrock: Advanced Graphing Designs](#beyond-the-basic-shamrock-advanced-graphing-designs)
- [Troubleshooting Your Shamrock Graphing Adventures](#troubleshooting-your-shamrock-graphing-adventures)
- [Integrating Shamrock Graphs into STEM Learning](#integrating-shamrock-graphs-into-stem-learning)
- [The Art of Customizing Your Shamrock Graph Printables](#the-art-of-customizing-your-shamrock-graph-printables)
- [Celebrating St. Patrick's Day with Math: Fun & Education Combined](#celebrating-st-patricks-day-with-math-fun--education-combined)
- [Resource Hub: Where to Find and Create Your Own](#resource-hub-where-to-find-and-create-your-own)
- [How to Choose the Best Coordinate Plane Shamrock Graph Printable for Your Needs](#how-to-choose-the-best-coordinate-plane-shamrock-graph-printable-for-your-needs)
- [Common Pitfalls to Avoid in Coordinate Plane Graphing](#common-pitfalls-to-avoid-in-coordinate-plane-graphing)
- [Advanced Tips for Experts: Elevating Your Graphing Game](#advanced-tips-for-experts-elevating-your-graphing-game)
- [Conclusion: Plot Your Path to Graphing Greatness](#conclusion-plot-your-path-to-graphing-greatness)
---
The Magic of the Coordinate Plane: A Beginner's Journey
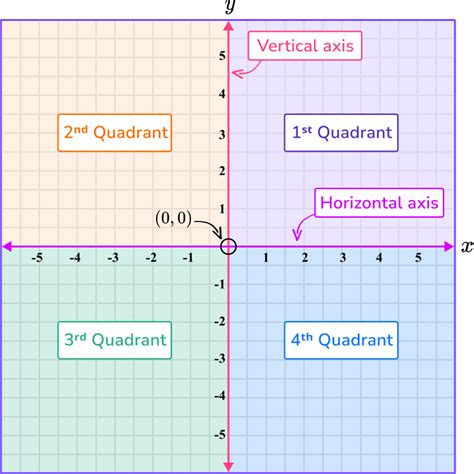
Before we dive into creating beautiful shamrocks, let's lay the groundwork. Understanding the coordinate plane is like learning the alphabet before writing a novel – it's the fundamental language of plotting. For many, this can feel intimidating, but I promise, it's an intuitive system once you grasp the basics. Think of it as a treasure map where every point has a unique address.
1. Understanding the X and Y Axes: Imagine two number lines, one horizontal (the X-axis) and one vertical (the Y-axis), crossing at their zero points. This intersection is called the origin (0,0). The X-axis tells you how far left or right to go, and the Y-axis tells you how far up or down. It's like navigating a city grid!
2. The Concept of Ordered Pairs (x,y): Every point on the coordinate plane is represented by an ordered pair, always written as (x, y). The first number, 'x', is your horizontal movement from the origin. The second number, 'y', is your vertical movement. For example, (3, 2) means move 3 units right, then 2 units up.
3. Positive and Negative Directions: Moving right on the X-axis means positive x-values; moving left means negative x-values. Moving up on the Y-axis means positive y-values; moving down means negative y-values. This is crucial for plotting complex shapes like our shamrock. I remember explaining this to a student by saying, "Think of it like money: positive is what you have, negative is what you owe!"
4. The Four Quadrants: The intersecting axes divide the plane into four sections, or quadrants, numbered counter-clockwise using Roman numerals.
- Quadrant I (+x, +y): Top-right. All points have positive x and positive y values.
- Quadrant II (-x, +y): Top-left. Points have negative x and positive y values.
- Quadrant III (-x, -y): Bottom-left. Points have negative x and negative y values.
- Quadrant IV (+x, -y): Bottom-right. Points have positive x and negative y values.
Understanding the quadrants helps you anticipate where your points will fall, especially when working with symmetrical designs like the shamrock.
5. Plotting Points: A Step-by-Step Guide:
- Start at the origin (0,0).
- Look at the x-coordinate: Move right for positive, left for negative.
- Look at the y-coordinate: From your current position, move up for positive, down for negative.
- Mark the point. Repeat! It’s simpler than it sounds.
6. Connecting the Dots to Form Shapes: Once you've plotted a series of points, you connect them in the order they're given (or in a logical sequence for a shape) to reveal the hidden image. This is where the magic truly happens! For beginners, I always recommend using a ruler for straight lines and a steady hand. My own first attempt at connecting dots was more abstract art than a recognizable shape, but practice truly makes perfect.
7. Real-World Applications of Coordinate Planes: It's not just for math class! Coordinate planes are used in GPS systems, video games, architecture, engineering, and even art. Showing kids these connections can spark their interest immediately.
8. The Importance of Scale: The grid lines on your coordinate plane shamrock graph printable represent units. Make sure you understand the scale – are they single units, or do they represent 2s, 5s, or 10s? This impacts how large or small your final image appears.
9. Gridded Paper vs. Freehand: While you *could* freehand, using gridded paper makes plotting much more accurate and less frustrating. That's why the "printable" aspect of our keyword is so valuable!
10. Practice Makes Perfect: Like any skill, plotting points requires practice. Start with simple shapes like squares or triangles before moving on to intricate designs like the shamrock. Don't get discouraged if your first few attempts aren't perfect; it's all part of the learning process.
Shamrock Graphing: From Concept to Clover

Now that you're comfortable with the coordinate plane, let's apply that knowledge to our beloved shamrock! A shamrock, with its three distinct heart-shaped leaves and a stem, is a fantastic target for a coordinate graphing project. It's complex enough to be engaging but not so overwhelming that it frustrates beginners.
1. Deconstructing the Shamrock Shape: A traditional shamrock consists of three overlapping heart-like shapes for the leaves and a short stem. Each "leaf" can be broken down into a series of points that, when connected, form its curve. The key is symmetry.
2. Point Lists: The Shamrock's Blueprint: To graph a shamrock, you'll work from a list of ordered pairs. Each segment of the shamrock (each curve of a leaf, or the stem) will have its own sequence of points. Some lists might even tell you when to "lift your pencil" to start a new part of the shape.
3. The Role of Symmetry in Shamrock Design: Shamrocks often exhibit radial symmetry. This means if you design one leaf, you can often derive the points for the other two by rotating or reflecting the coordinates. For instance, if one leaf is primarily in Quadrant I, another might be in Quadrant II, and the third might straddle Quadrants III and IV, all centered around the origin. This insight can save you a lot of time if you're trying to design your own.
4. Choosing Your Shamrock Complexity: You can find coordinate plane shamrock graph printable exercises ranging from simple, blocky shamrocks for younger learners to intricate, curvilinear designs for older students or those seeking a challenge. Start simple and build up! My first shamrock graph was quite angular, but it was incredibly satisfying to see it emerge from the dots.
5. Step-by-Step Plotting for a Leaf:
- Take the first set of points for one leaf.
- Plot each point carefully on your printable coordinate plane.
- Connect the points in the given order. This will form one part of the leaf's curve.
- Repeat for the next set of points, connecting them to the previous segment if indicated.
6. Adding the Stem: The stem is usually a straightforward series of points, often a straight line or a slight curve extending downwards from the center of the leaves. Don't forget this crucial detail!
7. Coloring and Decorating: Once your shamrock is plotted and all lines are connected, the real fun begins! You can color it green, add glitter, or even draw a pot of gold at the end of the stem. This artistic step transforms a math exercise into a creative project.
8. Understanding "Lift Pencil" Instructions: Some point lists will include instructions like "lift pencil" or "start new line." This means you plot the preceding points and connect them, then move to the next point without drawing a line between it and the previous point, effectively starting a new segment of the drawing.
9. Troubleshooting Common Shamrock Plotting Errors:
- Swapping X and Y: This is perhaps the most common mistake. Always remember (x, then y) – "walk before you climb."
- Incorrect Quadrant: Double-check your positive and negative signs.
- Skipping Points: Ensure you plot every point in the sequence.
- Connecting in the Wrong Order: Follow the list precisely.
10. The Satisfaction of the Reveal: There's a genuine sense of accomplishment when you connect the final point and the shamrock magically appears. It's a tangible result of applying mathematical principles, and that's a powerful learning experience. I still remember the "aha!" moment when my nephew, after much grumbling, finally saw his shamrock take shape. His grin was worth every minute of our shared struggle.
Unlocking the Power of Printable Shamrock Graphs

The term "coordinate plane shamrock graph printable" highlights the convenience and accessibility of these resources. Why draw your own grid or painstakingly create point lists when a ready-made solution is just a click away? Printables are a game-changer for educators, parents, and students alike.
1. Instant Access and Convenience: The primary benefit of a printable is its immediate availability. No need to wait for shipping or buy specialized books. A quick search, a download, and you're ready to go. This convenience factor is a huge plus for busy teachers and parents.
2. Variety of Designs: Printables come in a vast array of complexities and styles. You can find simple shamrocks for younger kids, intricate designs for a challenge, or even "mystery graphs" where the shape isn't revealed until all points are plotted. This variety ensures there's something for every skill level.
3. Cost-Effective Learning: Many coordinate plane shamrock graph printable resources are available for free online, making them an incredibly budget-friendly educational tool. You only pay for the paper and ink!
4. Differentiated Learning Made Easy: With a range of printables, you can easily cater to different learning paces and abilities within a classroom or home setting. Give simpler versions to those who need more practice and more complex ones to advanced learners.
5. Engaging Seasonal Activities: The shamrock theme makes these printables perfect for St. Patrick's Day, turning a regular math lesson into a festive celebration. This thematic approach makes learning more enjoyable and memorable. I've seen firsthand how a holiday theme can transform a student's attitude towards a subject.
6. Reinforcement of Math Concepts: Beyond the fun, these printables are powerful tools for reinforcing core math concepts:
- Understanding ordered pairs.
- Identifying positive and negative numbers.
- Navigating the coordinate plane.
- Developing fine motor skills through plotting and drawing lines.
7. Perfect for Homework or Independent Practice: A coordinate plane shamrock graph printable makes for excellent homework assignments or independent practice activities. Students can work at their own pace, and teachers can easily assess their understanding.
8. Boosting Confidence and Problem-Solving Skills: Successfully completing a coordinate graph art project gives students a tangible sense of accomplishment, boosting their confidence in math. It also subtly teaches problem-solving as they work through the point lists.
9. Beyond the Shamrock: A Gateway to Graphing Art: Once students master the shamrock, these printables can open the door to a whole world of graphing art, from animals and characters to famous landmarks. It shows them that math can be beautiful and creative.
10. Tips for Printing:
- Check Printer Settings: Ensure you print at "actual size" or 100% scale to maintain accurate grid proportions.
- Paper Quality: Use regular printer paper, but cardstock can be nice for a more durable project.
- Ink Levels: No one wants a faded graph!
- Accessibility: Consider if you need larger grids for students with visual impairments or fine motor challenges. Some printables offer different grid sizes.
Creative Classroom & Home Activities with Shamrock Graphs

The coordinate plane shamrock graph printable isn't just a worksheet; it's a springboard for a multitude of engaging activities. Whether you're a teacher looking to spice up your math lessons or a parent seeking fun, educational projects for your kids, these ideas will help you maximize the shamrock's potential.
1. "Mystery Shamrock" Reveal: Print the coordinate plane and point list separately. Students plot the points without knowing the final image. The "reveal" of the shamrock at the end is incredibly satisfying and adds an element of suspense. This was a huge hit in a class I once observed; the kids were buzzing with excitement as the shape emerged.
2. Collaborative Shamrock Mural: Divide a large coordinate plane into smaller sections. Assign each section to a different group or student with their own portion of the shamrock's point list. Once completed, assemble the sections to create a giant shamrock mural. This promotes teamwork and spatial reasoning.
3. Shamrock Scavenger Hunt: Hide parts of the point list around the classroom or house, with clues leading to the next set of coordinates. Students must find all the clues to complete their shamrock graph. This adds a physical activity dimension to the math task.
4. Shamrock Graphing Race: Provide multiple coordinate plane shamrock graph printable versions of varying difficulty. Students choose their challenge and race to accurately complete their shamrock. Emphasize accuracy over speed, but the competitive element can be motivating.
5. "Design Your Own Shamrock" Challenge: For advanced students, challenge them to create their *own* shamrock design on a blank coordinate plane and then generate the corresponding list of ordered pairs. This takes critical thinking and a deeper understanding of coordinates.
6. Shamrock Symmetry Exploration: After plotting the shamrock, have students identify lines of symmetry. Discuss how reflections work with coordinates (e.g., reflecting over the y-axis changes (x,y) to (-x,y)). This connects the graphing to geometric transformations.
7. 3D Shamrock Model (Extending the Plane): Once the 2D shamrock is complete, challenge students to think about how they could represent it in 3D. While not directly on the coordinate plane, it encourages spatial reasoning and connects to more advanced concepts like 3D graphing.
8. Shamrock Storytelling: Have students write a short story about their shamrock. Where did it come from? What magical properties does it have? This blends literacy with math and encourages creative expression. I once had a student write a story about a leprechaun who used the coordinate plane as his treasure map!
9. Coordinate Grid Games with a Shamrock Theme: Adapt classic games like Battleship or Connect Four using a coordinate plane backdrop and shamrock markers. This makes practicing coordinate identification fun and interactive.
10. Shamrock Graph Art Gallery: Once all students have completed their coordinate plane shamrock graph printable projects, display them prominently. This celebrates their hard work and showcases the diverse interpretations of the same mathematical instructions. Encourage peer feedback and appreciation for each other's work.
Beyond the Basic Shamrock: Advanced Graphing Designs

Once you've mastered the classic shamrock, the coordinate plane opens up a world of intricate and challenging graphing art projects. For those seeking to push their skills further, these ideas demonstrate the incredible versatility of coordinate graphing.
1. Complex Shamrock Variations: Move beyond the simple three-leaf design. Explore four-leaf clovers, shamrocks with intricate patterns within each leaf, or even a shamrock made of smaller, nested shamrocks. This requires longer point lists and more precise plotting.
2. Themed Coordinate Art: Apply the same principles to other seasonal or interest-based themes. Think Easter bunnies, Christmas trees, Halloween pumpkins, or even popular cartoon characters. The process remains the same: a list of points reveals the image.
3. Quadratic and Cubic Function Art: For more advanced learners, introduce the concept of plotting points generated by functions (e.g., y = x², y = x³). While a shamrock is usually a collection of line segments, advanced graphing art can involve smooth curves generated by equations.
4. Symmetry and Transformations: Deepen the understanding of symmetry by creating designs that require reflections, rotations, and translations of points. For example, design one quadrant of a complex symmetrical image, then apply transformation rules to generate the points for the other quadrants. This is a powerful way to visualize abstract mathematical concepts. I remember a college professor showing us how a complex fractal image could be generated from just a few simple rules, and it blew my mind!
5. Hidden Message Graphs: Instead of just an image, create a graph where certain points, when connected or highlighted, spell out a word or a secret message. This adds a puzzle element that's particularly engaging.
6. "Connect the Dots" with a Twist: Create a graph where some points are distractions or "red herrings." Students must identify which points belong to the main image based on a pattern or specific instructions, making the task more analytical.
7. Parametric Equations for Curves: For high school or college-level students, introduce parametric equations, where x and y are both defined by a third variable (often 't'). This allows for even more complex and smooth curves, opening up possibilities for truly artistic graphing.
8. Digital Graphing Tools: Explore online graphing calculators or software (like GeoGebra or Desmos) that allow you to input coordinates and see the plot instantly. This is great for experimentation and verifying manual plots. It also makes designing your own complex images much easier.
9. Graphing from an Image: Take a simple image (like a silhouette) and try to "trace" its outline by identifying key coordinate points. This reverses the process and hones observational skills and estimation.
10. Mathematical Art Exhibitions: Encourage students to create their own advanced graphing art pieces and host a "Mathematical Art Exhibition." This showcases their creativity and technical skills, fostering a sense of pride and accomplishment. It also demonstrates that math is far more than just numbers on a page.
Troubleshooting Your Shamrock Graphing Adventures

Even the most seasoned grapher encounters a hiccup now and then. Don't worry if your shamrock looks more like a wilted cabbage than a vibrant clover on your coordinate plane shamrock graph printable. Most errors are common and easily fixable. Here’s how to diagnose and overcome them.
1. The "Swapped Axes" Syndrome:
- Problem: Your shamrock looks stretched or squashed, or points are consistently in the wrong place, but the numbers seem right. You've likely plotted (y, x) instead of (x, y).
- Solution: Always remember "x comes before y" – you "walk" horizontally (x) before you "climb" vertically (y). Double-check every single ordered pair as you plot it. This is the absolute classic mistake; don't be like me and spend half an hour wondering why your drawing is mirrored!
2. Sign Slip-Ups:
- Problem: Points are in the correct quadrant, but they're reflected across an axis, or entirely in the wrong quadrant.
- Solution: A common culprit is misinterpreting positive and negative signs. Remember: right and up are positive; left and down are negative. A quick review of the four quadrants and their sign conventions can fix this.
3. Missing or Skipped Points:
- Problem: Gaps in your drawing, or lines that don't connect properly.
- Solution: Go back to your point list and mark off each point as you plot it. Use a ruler to ensure your lines extend precisely to the plotted point. Sometimes, a point is just tiny and easily missed.
4. Connecting in the Wrong Order:
- Problem: Your shamrock resembles abstract art more than a clover, with lines crisscrossing unexpectedly.
- Solution: Pay close attention to the sequence of points. If the list indicates "lift pencil" or "start new segment," ensure you follow those instructions. Sometimes, it helps to number the points on the list as you plot them to keep track.
5. Grid Scale Confusion:
- Problem: Your shamrock is either too small and compressed, or too large and goes off the page.
- Solution: Verify the scale of your coordinate plane shamrock graph printable. Are the grid lines representing single units, or are they counting by 2s, 5s, or 10s? Adjust your plotting accordingly.
6. "Off-Grid" Points:
- Problem: You have a point like (3.5, 2.75) on a grid that only shows whole numbers.
- Solution: For beginner-level printables, points are usually whole numbers. If you encounter decimals, you'll need to estimate their position between the grid lines. If your printable is designed for whole numbers, double-check your point list for errors.
7. Faint Lines or Incorrect Tools:
- Problem: Your plotted points are hard to see, or your lines are wobbly.
- Solution: Use a sharp pencil (or a fine-tip marker for the final trace). A ruler is your best friend for connecting points accurately and neatly. Don't press too hard initially in case you need to erase.
8. Perfectionism Paralysis:
- Problem: You're so worried about making a mistake that you're afraid to even start.
- Solution: Embrace the process! Mistakes are how we learn. Keep an eraser handy, take a deep breath, and remember that the goal is understanding and enjoyment, not a museum-quality drawing on your first try. I tell my students, "It's not about being perfect, it's about being brave enough to try!"
9. Lack of Focus/Distractions:
- Problem: Errors accumulate because attention wanders.
- Solution: Find a quiet space. Plotting coordinates requires focus. Put on some calm music if it helps, and break the task into smaller chunks if it feels overwhelming.
10. When All Else Fails: Re-Start (Strategically):
- Problem: Your shamrock is completely off, and you can't pinpoint the error.
- Solution: Sometimes, it's quicker and less frustrating to start fresh on a new coordinate plane shamrock graph printable. Before you do, try to identify *where* you think the error might have occurred (e.g., "I think I messed up Quadrant II"). This makes the restart more productive.
Integrating Shamrock Graphs into STEM Learning

The coordinate plane shamrock graph printable isn't just a fun holiday activity; it's a versatile tool that can seamlessly integrate into broader STEM (Science, Technology, Engineering, and Mathematics) learning objectives. It provides a tangible link between abstract mathematical concepts and real-world applications.
1. Mathematical Foundations (M):
- Coordinate Geometry: Directly teaches plotting, ordered pairs, axes, and quadrants. This is the cornerstone of many higher-level math topics.
- Geometry & Transformations: Introduces concepts of shape, symmetry, and can be extended to reflections, rotations, and translations.
- Algebraic Thinking: For older students, creating point lists can lead to understanding how equations can generate shapes.
2. Spatial Reasoning (E - Engineering & M - Math):
- Blueprint Interpretation: Reading a list of coordinates is akin to reading a blueprint or a set of architectural plans, teaching students to translate abstract data into a physical representation.
- Design & Planning: Students learn to plan their steps, visualize the final product, and troubleshoot when their drawing doesn't match their expectation. This is fundamental to engineering design.
3. Data Visualization (S - Science & T - Technology):
- Graphing Data: While a shamrock is art, it teaches the fundamental skill of plotting data points, which is essential in all scientific fields for analyzing experiments and presenting findings.
- Spreadsheet Integration: For advanced learners, coordinates can be generated in a spreadsheet (Excel, Google Sheets), introducing them to basic data management and computational tools. This is a practical skill for future tech careers. I vividly remember how much easier data analysis became once I learned to visualize trends on a graph.
4. Computational Thinking (T - Technology):
- Algorithmic Thinking: The point list is essentially an algorithm – a set of instructions to achieve a specific outcome. Students learn to follow and, eventually, create algorithms.
- Programming Concepts: Understanding coordinates is vital for computer graphics and game development. A simple shamrock can be the first step towards writing code that draws shapes on a screen.
5. Problem-Solving (All STEM Fields):
- Debugging: When a shamrock doesn't look right, students must "debug" their work, systematically checking for errors in plotting or interpretation. This iterative process is at the heart of STEM problem-solving.
- Critical Thinking: Analyzing why a point should be in a certain quadrant or how a line segment contributes to the overall shape develops critical thinking skills.
6. Interdisciplinary Connections (All STEM Fields):
- Science: Graphing biological data (e.g., plant growth over time).
- Technology: Creating simple graphical user interfaces (GUIs).
- Engineering: Designing prototypes or mapping out structures.
- Math: The core subject, providing the tools.
7. Art as a Bridge to STEM:
- STEAM Integration: By adding the "A" for Art, we make STEM more accessible and appealing. The visual outcome of the shamrock graph highlights the beauty and creativity inherent in mathematical principles.
- Engagement: Using a fun, artistic project like the coordinate plane shamrock graph printable can draw in students who might otherwise be intimidated by traditional math problems.
8. Encouraging Exploration:
- Once the basic shamrock is mastered, encourage students to explore other coordinate art projects or even design their own. This fosters curiosity and a desire for deeper learning in STEM.
9. Real-World Context:
- Discuss how coordinate systems are